A star is a widely understood symbol used for ratings. If you’re building a UI for rating in an app, chances are you’ll be using a star in there somewhere. There are many different ways to get a star on the screen in your app, but the best way is to draw it from scratch in code. Not only does this give you total flexibility in terms of size and screen resolution and the ability to create awesome effects using core animation, it also allows you to totally nerd out on geometry. You can point to articles like this the next time someone dares to question why you learn all that stuff at school because “you’ll never use it in real life”.
Circles
Start with the classic five-pointed star. A star fits inside a circle. The point of the star goes straight up. There are 2𝛑 radians in a complete circle, so each other point hits the circle 2𝛑 / 5 radians round from the one before:
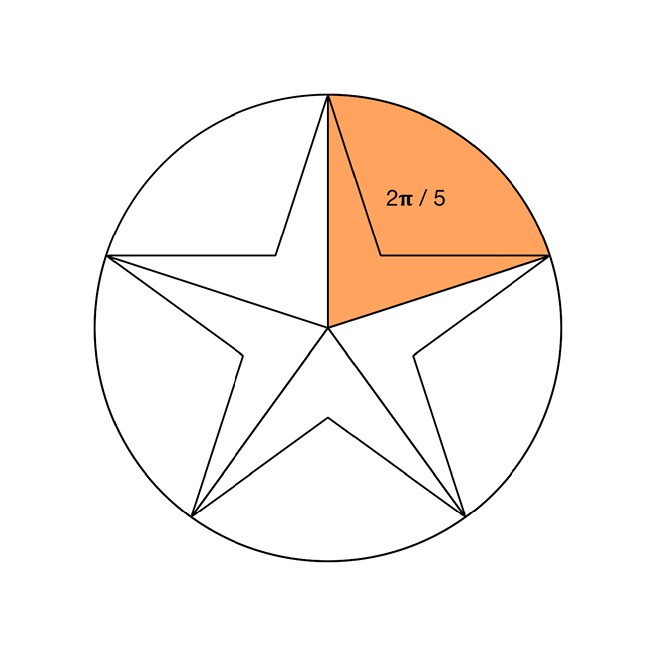
To calculate the coordinates of each point around the edge of the circle, I can use UIBezierPath’s addArc method. I’m not interested in the arcs themselves, but the currentPoint of the path as you add each arc will be the point of interest. This extension on UIBezierPath gives me what I need:
extension UIBezierPath {
static let twelveOClock: CGFloat = .pi * 1.5
class func pointsOnCircle(
center: CGPoint,
radius: CGFloat,
points: Int,
startAngle: CGFloat = twelveOClock) -> [CGPoint] {
let pointOffsetAngle = ((.pi * 2.0) / CGFloat(points))
var startAngle = startAngle
var endAngle = startAngle
let path = UIBezierPath()
path.move(to: .zero)
var circlePoints = [CGPoint]()
for _ in 1...points {
path.addArc(withCenter: center, radius: radius, startAngle: startAngle, endAngle: endAngle, clockwise: true)
circlePoints.append(path.currentPoint)
startAngle = endAngle
endAngle += pointOffsetAngle
}
return circlePoints
}
}
Once I get the points, I can draw the star by connecting points on the circle as shown here, starting at 1 and working up to 5, then returning to 1:
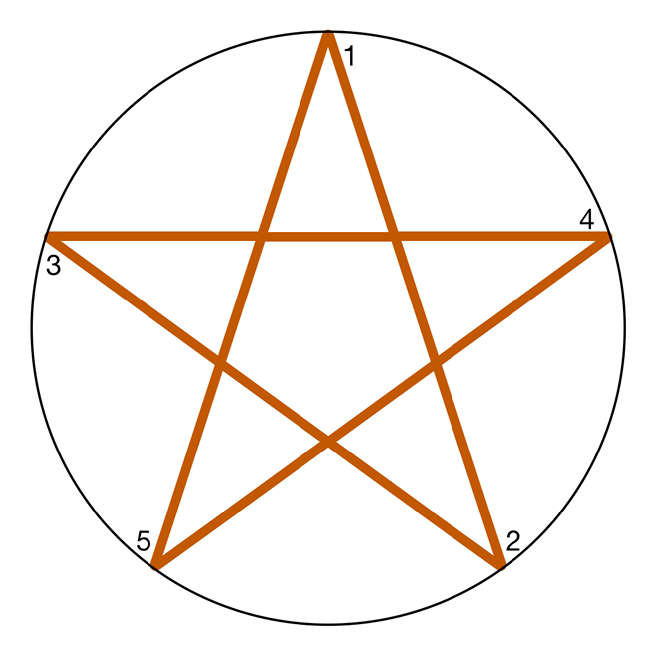
Drawing a star like this doesn’t give the right result. It’s fine if all I want to do is fill the path, but if I want to have empty or partially filled stars (to represent an average rating of 3.6 stars, for example) then this path isn’t going to work. There’s all that mess in the middle which I don’t want to see. How can I calculate where those inner points are going to be? It’s time to bust out some trigonometry.
Triangles
Trigonometry is all about right angled triangles, and at first glance there aren’t any in the diagram. But that’s only because I haven’t drawn enough extra lines on it. I can make a larger pentagon by joining all of the outer points of the star, and I can draw a line from the center of the circle that passes through the inner point. That gives me something like this:
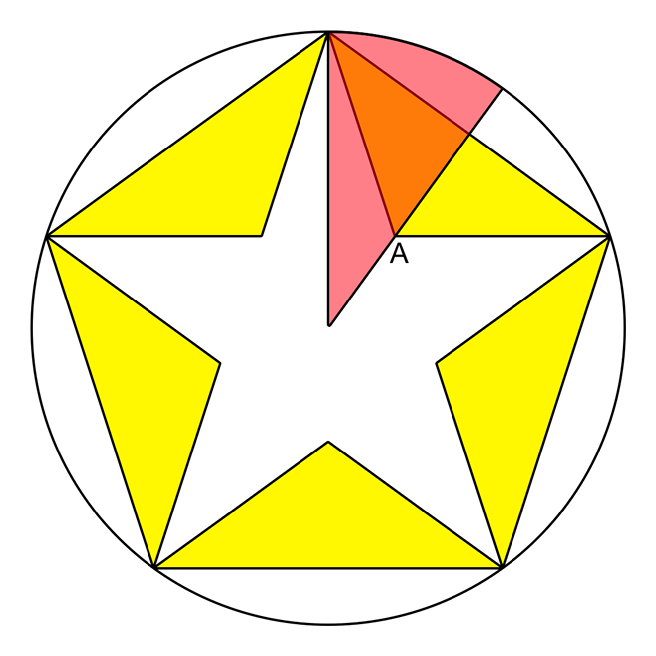
The orange area is a right angled triangle! However, I don’t know enough about it. To describe a right-angled triangle I need at least two numbers out of:
- The lengths of the sides
- The non-right angles
Currently I can calculate only the length of one side - the side that goes halfway along the edge of that large pentagon. I can do that using this extension on CGPoint for calculating midpoints and distances. The distance method uses Pythagoras’ theorem, so you’re damn right it gets used in real life!:
extension CGPoint {
func distance(to: CGPoint) -> CGFloat {
let deltaX = Double(to.x - self.x)
let deltaY = Double(to.y - self.y)
let distance = sqrt((deltaX * deltaX) + (deltaY * deltaY))
return CGFloat(distance)
}
func midPoint(to: CGPoint) -> CGPoint {
let deltaX = to.x - self.x
let deltaY = to.y - self.y
return self.applying(CGAffineTransform(translationX: deltaX * 0.5, y: deltaY * 0.5))
}
}
What I want to do is work out where the inner points of the star should be, so I can draw straight to them instead of relying on lines crossing over. To do this I need to find out the distance from the centre of the circle to the inner point of the star. The inner point is highlighted in blue on the diagram above.
Pentagons
In the centre of the five-pointed star is a pentagon. That isn’t a coincidence. At the centre of a six-pointed star you’ll find a hexagon, and so on. Here’s a geometry fact you may have forgotten since school (I certainly had): you can find the internal angles of a regular polygon, such as a pentagon, with this formula: ((n - 2) * 𝛑) / n, where n is the number of sides. Here are the internal angles of a pentagon:
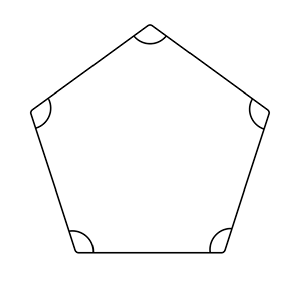
Each of the marked angles is therefore 3𝛑 / 5. Why do I care about this? Take a closer look at the inner point, with the pentagon visible:
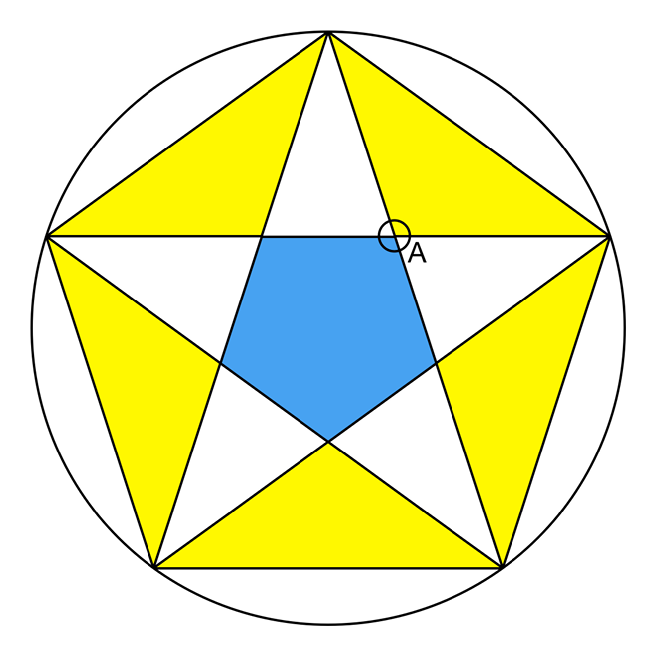
Consider the circle over the inner point. The blue section of the circle matches the internal angle of the pentagon. The bottom right is 𝛑 - that value, because that’s how many radians there are in half a circle. Those values are mirrored in the top half of the circle, so the yellow section of the circle is the same as the internal angle of the pentagon. The top right yellow section is the angle I’m interested in - the edge of the triangle passes through this, and because the edge ends at the mid-point of the line between the two outer points, I know that the edge cuts that yellow angle in half - so I now have one of the internal angles of my triangle! This is enough information for me to calculate everything I need to know.
The terms used in describing a right-angled triangle are:
- Hypotenuse - the edge of the triangle that is opposite the right angle
- 𝜃 (theta) - the non-right angle you’re interested in
- Opposite - the edge of the triangle opposite 𝜃
- Adjacent - the edge of the triangle next to 𝜃
As said earlier, I need any two of these pieces of information. I have 𝜃, which is half of the internal angle of a pentagon, or (3𝛑 / 5) / 2 (simplified to 0.3𝛑 if you like) and I have the length of the opposite side. I’m interested in the length of the adjacent side.
This diagram shows the various parts of the triangle:
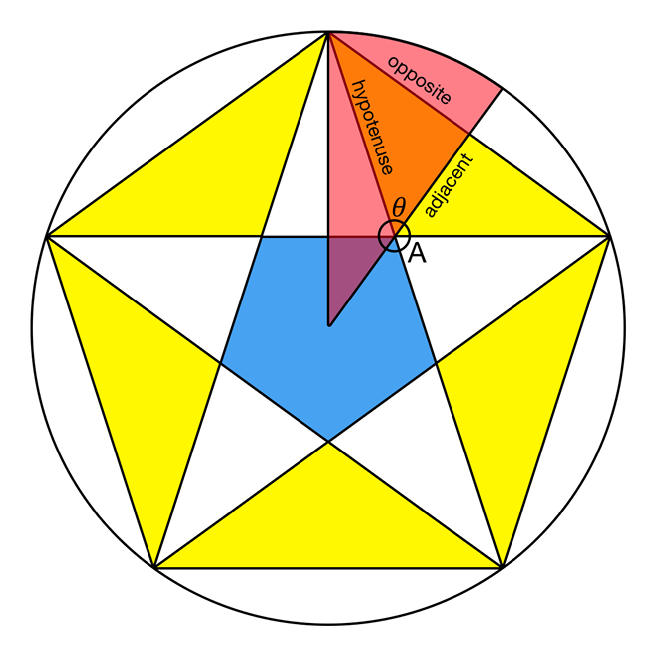
There are three trigonometry formulae you may have been forced to memorise at school. The one involving opposite and ajacent sides is this:
Tan 𝜃 = opposite / adjacent
I need to put the two things I know on the same side, so I can work out the thing I don’t know, which means the formula needs to be rearranged to:
adjacent = opposite / Tan 𝜃
This gives me the distance from the inner point to the midpoint of the two outer points. I actually care about the distance from the center of the circle to the inner point, but that’s easy to calculate with my CGPoint extension.
I now have the radius of another, smaller circle, which has all the inner points along its circumference. This means I can use my pointsOnCircle method again, passing in the new radius and a different start angle (halfway between the first two outer points). Here’s the inner circle:
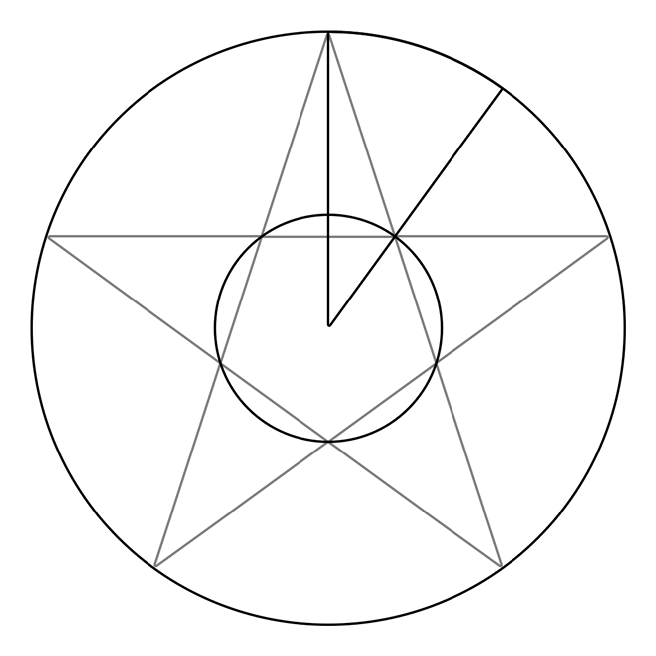
Combining the two arrays of points into a single path gives me a perfect star, with no messy internal lines. ★★★★★ for geometry!
The code
This exension gives a new initializer to UIBezierPath which returns a star of a given number of points, inside a given rectangle. It depends on the other extensions earlier in the article:
extension UIBezierPath {
convenience init(starIn rect: CGRect, points: Int = 5) {
precondition(points >= 3, "Invalid number of points")
// Constants describing the star
let center = CGPoint(x: rect.midX, y: rect.midY)
let radius = rect.size.width * 0.5
let outerPoints = UIBezierPath.pointsOnCircle(center: center, radius: radius, points: points)
// This calculation works out the distance from a line between the first two outer
// points and the first inner point
// The internal angle of the regular polygon at the center of the star
let internalAngle: CGFloat = (CGFloat(points - 2) * .pi) / CGFloat(points)
// The midpoint of the line between the two outer points
let midPoint = outerPoints[0].midPoint(to: outerPoints[1])
// The length of that line
let opp = outerPoints[0].distance(to: midPoint)
let theta = internalAngle * 0.5
let distanceIn = opp / tan(theta)
// This then gives us the radius of the inner circle
let innerRadius: CGFloat
switch points {
case 3, 4: innerRadius = center.distance(to: midPoint) * 0.5
default: innerRadius = center.distance(to: midPoint) - distanceIn
}
// We can now repeat the arc circles trick to give us the points on the inner circle. The start angle needs to be adjusted as it won't be at the top of the circle, but halfway between two outer points
let innerPointOffset = (.pi * 2.0 / CGFloat(points)) * 0.5
let innerPoints = UIBezierPath.pointsOnCircle(center: center, radius: innerRadius, points: points, startAngle: UIBezierPath.twelveOClock + innerPointOffset)
// Finally use the two sets of points to create the path
self.init()
self.move(to: outerPoints[0])
for (outer, inner) in zip(outerPoints, innerPoints) {
self.addLine(to: outer)
self.addLine(to: inner)
}
self.close()
// Center the star vertically in the passed in rect
let starBounds = self.bounds
let heightAdjustment = (rect.height - starBounds.height) * 0.5
self.apply(CGAffineTransform(translationX: 0, y: heightAdjustment))
}
}
One way you could use this code would be to draw an image of a star - here’s a way to draw a partially filled star:
extension UIImage {
class func star(of size: CGSize, color: UIColor, points: Int = 5, filled: CGFloat = 1.0) -> UIImage {
let renderer = UIGraphicsImageRenderer(size: size)
let image = renderer.image { rendererContext in
let bounds = rendererContext.format.bounds
let starPath = UIBezierPath(starIn: bounds.insetBy(dx: 2, dy: 2), points: points)
starPath.lineWidth = 4
color.setStroke()
starPath.stroke()
starPath.addClip()
var fillRect = bounds
fillRect.size.width *= filled
color.setFill()
UIRectFill(fillRect)
}
return image
}
}
UIImage.star(of: CGSize(width: 200, height: 200), color: .orange, points: 5, filled: 0.6)
Gives you:

The star path is more flexible and offers better performance when used in conjunction with a CAShapeLayer. That implementation is left as an exercise for the reader.
Conclusion
Having geometric forms as bezier paths gives you total flexibility for UI design and makes changes to size, styling and color straightforward.
It’s possible to make almost any geometric form in code, but you may need to dust off some school geometry to get there. And you might even have fun doing it!


